Rumus Tabung: Cara Menghitung Volume, Luas Permukaan & Contoh soal
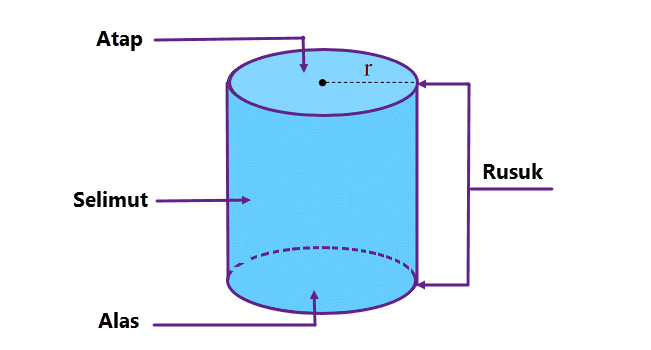
Rumus Tabung – Dalam kehidupan sehari-hari pastinya anda sering menemukan berbagai bangun ruang termasuk salah satunya adalah tabung. Perlu anda ketahui bahwa tabung merupakan bangun ruang yang mempunyai alas serta tutup yang berbentuk lingkaran dan selimut lengkung yang berbentuk persegi panjang.
Setiap bangun ruang pasti memiliki volume dan luas permukaan yang juga berlaku pada tabung. Untuk itulah tabung memiliki rumus yang terdiri dari rumus volume dan rumus luas permukaan tabung. Dengan rumus tersebut maka anda akan semakin mudah dalam menentukan volume serta luas permukaan tabung tanpa perlu repot.
Sebelum anda mempelajari tentang rumus tabung yang terdiri dari rumus volume dan luas permukaan maka ketahui terlebih dahulu sifat-sifat tabung. Dimana sifat-sifat tersebut yaitu mempunyai alas serta tutup yang berukuran sama, mempunyai 2 rusuk, mempunyai 3 bidang yaitu 2 lingkaran dan 1 persegi panjang serta tidak mempunyai titik sudut.
Melalui sifat-sifat inilah maka rumus volume serta luas permukaan tabung bisa diperoleh hingga akhirnya memudahkan anda ketika akan menghitung keduanya.
Daftar Isi
Rumus Tabung untuk Menghitung Volume
Seperti yang sudah dijelaskan sebelumnya bahwa sebuah tabung memiliki alas serta tutup yang bentuknya berupa lingkaran. Untuk itulah rumus tabung menghitung volume bisa dilakukan dengan menghitung alas serta tinggi tabung tersebut.
Cukup dengan mengalikan tinggi dan luas alas tabung maka akan diperoleh volume tabung. Untuk lebih mudahnya berikut ini rumus volume tabung yang perlu anda pahami :
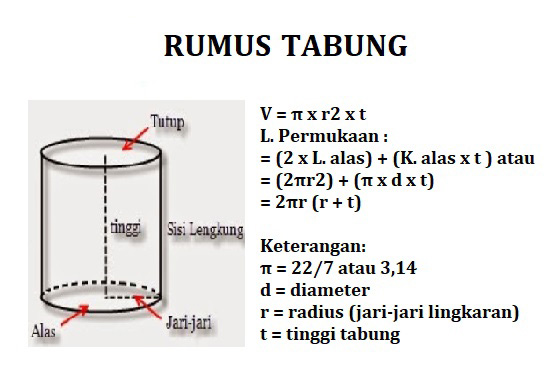
V = π x r2 x t
Keterangan :
V = Volume
π = 22/7 atau 3,14
r = radius atau jari-jari lingkaran
t = tinggi tabung
Contoh Soal Menghitung Volume Tabung
Berikut ini beberapa contoh soal untuk menghitung volume tabung:
Contoh Soal 1
Jika sebuah tabung memiliki jari-jari alasnya yaitu 7 cm serta tingginya tabung 14 cm maka tentukan volume tabung tersebut !
Jawab:
r = 7cm
t = 14 cm
V = π x r2 x t
= 22/7 x 7 x 7 x 14
= 2.156 cm3
Jadi volume tabung tersebut adalah 2.156 cm3.
Contoh Soal 2
Kayu berbentuk silinder memiliki luas penampang 240 cm2. Silinder kayu tersebut tingginya 50 cm. Hitung volume kayu berbentuk silinder tersebut?
Jawab :
Volume silinder kayu = 240 cm2 x 50 cm = 12.000 cm³.
Contoh Soal 3
Terdapat sebuah besi batangan dengan panjang 7 meter dengan penampang berbentuk lingkaran dengan diameter 1 cm. Hitunglah volume batang besi tersebut dalam centimeter kubik?
Jawab :
Panjang besi = tinggi silinder yaitu 7 m = 700 cm.
Radius silinder = setengah kali diameter batang besi yaitu 0,5 cm.
Volume batang besi = (22/7) x 0,5 cm x 0,5 cm x 700 cm = 550 cm³.
Contoh Soal 4
Uang logam memiliki tebal 1,4 mm dan diameter 20 mm. Hitung volume koin tersebut!
Jawab :
Tebal koin = tinggi silinder yaitu 1,4 mm.
Radius koin = setengah kali diameter yaitu 10 mm.
Volume koin = (22/7) x 10 mm x 10 mm x 1,4 mm = 440 mm³.
Rumus Menghitung Luas Permukaan Tabung
Setelah anda mengetahui rumus volume tabung maka selanjutnya anda juga perlu mengetahui rumus luas permukaan tabung. Dimana untuk luas permukaan tabung bisa diperoleh dari luas jumlah sisi yang dimiliki oleh tabung.
Jumlah sisi pada tabung sama dengan bidang yang membentuk tabung tersebut. Dalam sebuah tabung terdiri dari 3 bidang yaitu 2 lingkaran alas dan tutup serat selimut tabung berbentuk persegi panjang.
Perlu anda ketahui bahwa luas permukaan tabung ternyata berpengaruh pada besar atau kecilnya sebuah tabung. Dengan demikian rumus tabung untuk luas permukaan bisa dirumuskan sebagai berikut :
Lp = 2 π r 2 + 2 π r t
= 2 π r (r + t)
Keterangan :
Lp = luas permukaan
V = Volume
π = 22/7 atau 3,14
r = radius atau jari-jari lingkaran
t = tinggi tabung
Contoh Soal Menghitung Luas Permukaan Tabung
Sebuah tabung memiliki jari-jari 20 cm dengan tinggi tabung yaitu 40 cm. Maka hitunglah luas permukaan tabung tersebut !.
Jawab :
r = 20 cm
t = 40 cm
Lp = 2 π r 2 + 2 π r t
= 2 x 3,14 x 20x 20 + 2 x 3,14 x 20 x 40
= 2.152 + 5.024
= 7.178 cm2
Jadi luas permukaan tabung tersebut adalah 7.178 cm2.
*****
Demikianlah penjelasan mengenai rumus tabung untuk menghitung volume dan luas permukaannya. Semoga bisa menambah wawasan anda. Melalui penjelasan di atas kini anda tak perlu bingung jika dihadapkan pada soal matematika untuk bangun ruang tabung. Sebab soal-soal tersebut bisa anda selesaikan secara mudah menggunakan rumus-rumus di atas.