Rumus Balok – Luas Sisi, Volume, Diagonal Ruang Bidang
Rumus Balok – Sejak duduk di bangku Sekolah Dasar, pasti anda sudah pernah belajar tentang balok. Seperti yang telah diketahui bahwa balok merupakan bangun ruang 3 dimensi yang dibentuk dari tiga pasang persegi atau persegi panjang yang memiliki sepasang rusuk yang berbeda.
Pada sebuah balok terdapat 6 sisi, 12 rusuk serta 8 titik sudut. Tentunya karena merupakan bangun ruang, balok juga memiliki volume atau isi serta bisa dihitung pula luas permukaannya seperti bangun ruang lainnya. Untuk itulah agar anda semakin mudah dalam menghitung volume atau luas permukaan sebuah balok maka terdapat rumus balok yang perlu anda ketahui.
Daftar Isi
Sifat-sifat Balok
- Mempunyai sisi-sisi yang berbentuk persegi panjang.
- Rusuk-rusuk balok yang sejajar mempunyai ukuran yang sama panjang.
- Masing-masing diagonal bidang pada sisi yang berhadapan mempunyai ukuran yang sama panjang.
- Masing-masing diagonal ruang balok mempunyai ukuran yang sama panjang.
- Masing-masing bidang diagonal pada balok mempunyai bentuk persegi panjang.
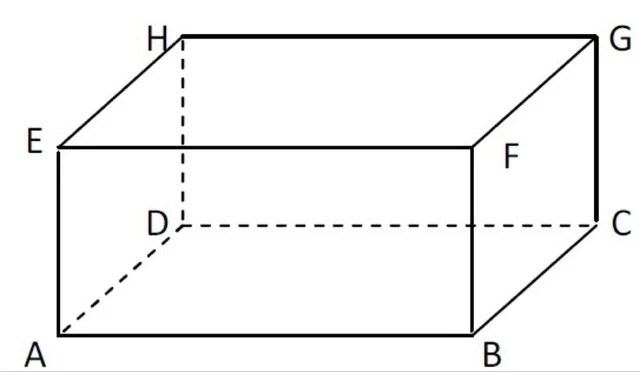
Unsur-Unsur Balok
Selain memiliki sifat-sifat seperti yang sudah dijelaskan di atas, balok juga terdiri dari unsur-unsur. Dimana dengan memahami unsur-unsur pada balok tersebut anda juga akan semakin mudah dalam memahami rumus balok. Unsur-unsur pada balok diantaranya sebagai berikut.
- Sisi atau Bidang
Sisi balok merupakan bidang yang membatasi balok yang jumlahnya ada 6 sisi untuk setiap balok. Dengan demikian dalam sebuah balok terdapat 3 pasang sisi yang sama ukuran dan bentuk. - Rusuk
Rusuk merupakan garis potongan antar dua sisi bidang balok yang tampak seperti kerangka penyusun balok. Tidak berbeda dengan kubus, balok ternyata juga memiliki 12 rusuk. - Titik Sudut
Titik sudut merupakan titik potongan antara dua atau bahkan 3 rusuk dan pada balok terdapat 8 titik sudut. - Diagonal Bidang
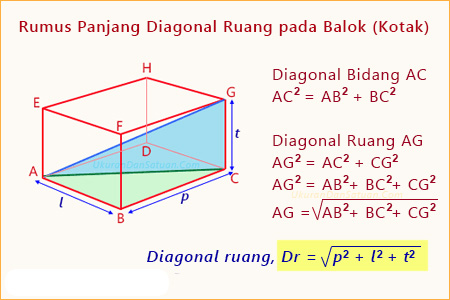
Diagonal bidang merupakan ruas garis yang menghubungkan antara dua titik sudut tang saling berhadapan disetiap bidang atau sisi balok. Sama seperti pada kubus, untuk balok mempunyai 12 diagonal bidang. - Diagonal Ruang
Diagonal ruang merupakan garis yang menghubungkan 2 titik sudut dan saling berhadapan dalam sebuah ruang. Untuk balok terdapat 4 diagonal ruang sama seperti pada kubus. - Bidang Diagonal
Bidang diagonal merupakan bidang yang dibatasi oleh dua diagonal bidang serta dua rusuk. Dalam sebuah balok terdapat 6 bidang diagonal yang sama seperti pada kubus.
Jenis- jenis Rumus Balok
Melalui penjelasan di atas maka kini anda bisa lebih memahami tentang balok sehingga memudakan anda dalam menggunakan rumus balok diantaranya sebagai berikut.
Rumus Luas Permukaan Balok
Lp = 2 ((pxl) + (pxt)+ (lxt))
Rumus Volume Balok
V = p x l x t
Luas Bidang Diagonal
Lb1 = Db1 x t
Lb2 = Db2 x t
Lb3 = Db3 x t
Contoh Soal Kubus
Sebuah balok memiliki panjang 5cm, lebar 3cm dan tinggi 4cm, maka tentukan volume dan luas permukaan balok tersebut !
Jawab :
p = 5cm
l = 3cm
t = 4 cm
V = p x l xt
= 5 x 3 x 4
= 60 cm3
Lp = 2 ((pxl) + (pxt)+ (lxt))
= 2 ((5×3) +(5×4) + (3×4))
= 2 (15 + 20 + 12 )
= 2 x 47
= 94 cm2
Demikianlah penjelasan mengenai mengenal sifat, unsur dan rumus balok yang bisa menambah wawasan anda. Bagi anda yang ingin mengerjakan soal-soal yang berhubungan dengan balok maka pahami penjelasan di atas supaya soal-soal yang anda miliki bisa dikerjakan secara tepat dan benar.
Ternyata menghitung luas bidang, diagonal atau volume balok itu sangat mudah ya. Sekarang kita bisa lebih cepat memahami pelajaran di sekolah dengan sarana web ini!