Kumpulan Contoh Soal Induksi Matematika

Matematika MIPA
June 12, 2023
0
8 minutes read

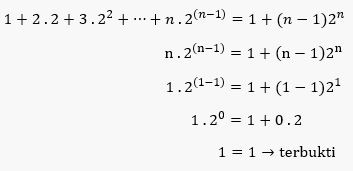
Contoh Soal Induksi Matematika – Halo sobat Jadi Juara dimanapun anda berada. Sebelumnya kami ucapkan selamat datang kepada anda semua yang berkenan mampir di web sederhana kami ini.

Web JadiJuara.com ini kami dedikasikan untuk perkembangan dunia pendidikan di Indonesia. Baik itu dunia pendidikan sekolah dasar, mengah atas sampai ke perguruan tinggi.

Kami berharap dengan adanya wbe ini bisa membantu anda semua untuk bisa menyelesaikan berbagai masalah di sekolah serta bisa menjadi referensi untuk anda belajar.

Kali ini JadiJuara akan berbagi tema seputar matematika, kita akan kupas seputar contoh soal induksi matematika. Untuk definisi Induksi Matematika sendiri adalah suatu metode pembuktian yang absah dalam metode Matematika.

Langkah-langkah Induksi Matematika adalah sebagai berikut:

p(n) = 1 adalah benar —> (basis).
Misalkan, kita asumsikan p(n) adalah benar —> (induktif).
p (n +1), juga harus benar.

Daftar Isi

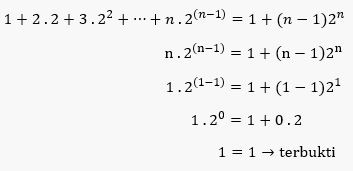
1 Contoh Soal Induksi Matematika 1:
2 Contoh Soal Induksi Matematika 2
3 Contoh Soal Induksi Matematika 3

Contoh Soal Induksi Matematika 1:

Misalkan:

induksi matematika

Contoh Soal Induksi Matematika 2

Perhatikan tabel berikut ini!

Bilangan Genap ke-n	Penjumlahan Bilangan Genap	Hasil	Terkaan
1	2	2	1 x 2
2	2 + 4	6	2 x 3
3	2 + 4 + 6	12	3 x 4
4	2 + 4 + 6 + 8	20	4 x 5
…	…	…	…
n	2 + 4 + 6 + 8 + … + 2n	…	n(n + 1)

Sehingga didapat:

2 + 4 + 6 + 8 + … + 2n = n(n + 1)

Maka Induksi Matematikanya:

1. P (1) = n(n+1)

= 1 (1 + 1)

= 1 . 2

= 2 —> Benar

2. P (n) = n(n + 1)

Misalkan n = 3

P (3) = 3 (3 +1)

= 3 . 4

= 12 —> Benar

3. Untuk P (n + 1)

2 + 4 + 6 + 8 + … + 2n = n(n + 1)

Maka:

2 + 4 + 6 + 8 + … + 2n + 2n = (n + 1) ((n + 1) + 1)

= (n + 1) (n +2)

Sehingga (gunakan sifat-sifat bilangan):

2 + 4 + 6 + 8 + … + 2n + 2n = (2 + 4 + 6 + 8 + … + 2n) + 2n

= n(n + 1) + 2(n + 1)

= (n + 1) (n +2)

Terbukti! Antara ruas kanan dan ruas kiri sama.

Contoh Soal Induksi Matematika 3

Gunakan induksi matematika untuk membuktikan rumus

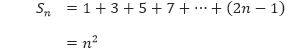
Soal 2

untuk semua bilangan bulat n ≥ 1.

Pembahasan Induksi matematika terdiri dari dua bagian yang berbeda.

Pertama, kita harus menunjukkan bahwa rumus tersebut benar ketika n = 1. Ketika n = 1, rumus tersebut benar, karena
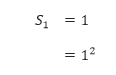
Bagian kedua induksi matematika memiliki dua langkah. Langkah pertama adalah menganggap bahwa rumus tersebut benar untuk sebarang bilangan bulat k. Langkah kedua adalah menggunakan anggapan ini untuk membuktikan bahwa rumus tersebut benar untuk bilangan bulat selanjutnya, k + 1. Anggap bahwa rumus

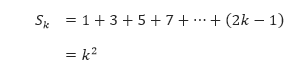
bernilai benar, kita harus menunjukkan bahwa rumus S_k_{+ 1} = (k + 1)² benar.

Dengan menggabungkan hasil pada langkah (1) dan (2), kita dapat menyimpulkan dengan induksi matematika bahwa rumus tersebut benar untuk semua bilangan bulat n ≥ 1.

Semoga dengan contoh di atas sudah bisa menjelaskan contoh soal induksi matematika kepada anda.

Matematika pada dasarnya memang adalah latihan soal, semakin banyak kita berlatih mengerjakan soal matematika, maka kita bisa semakin mahir dan cepat dalam menyelesaikan berbagai soal yang diberikan. Tunggu contoh soal matematika lainnya ya. Selamat belajar!